Platonic solids

How to use this exercise?

Convex regular polyhedra - Show in 3D the polyhedral geometrics.

Number of pieces of this exercise

5

General description

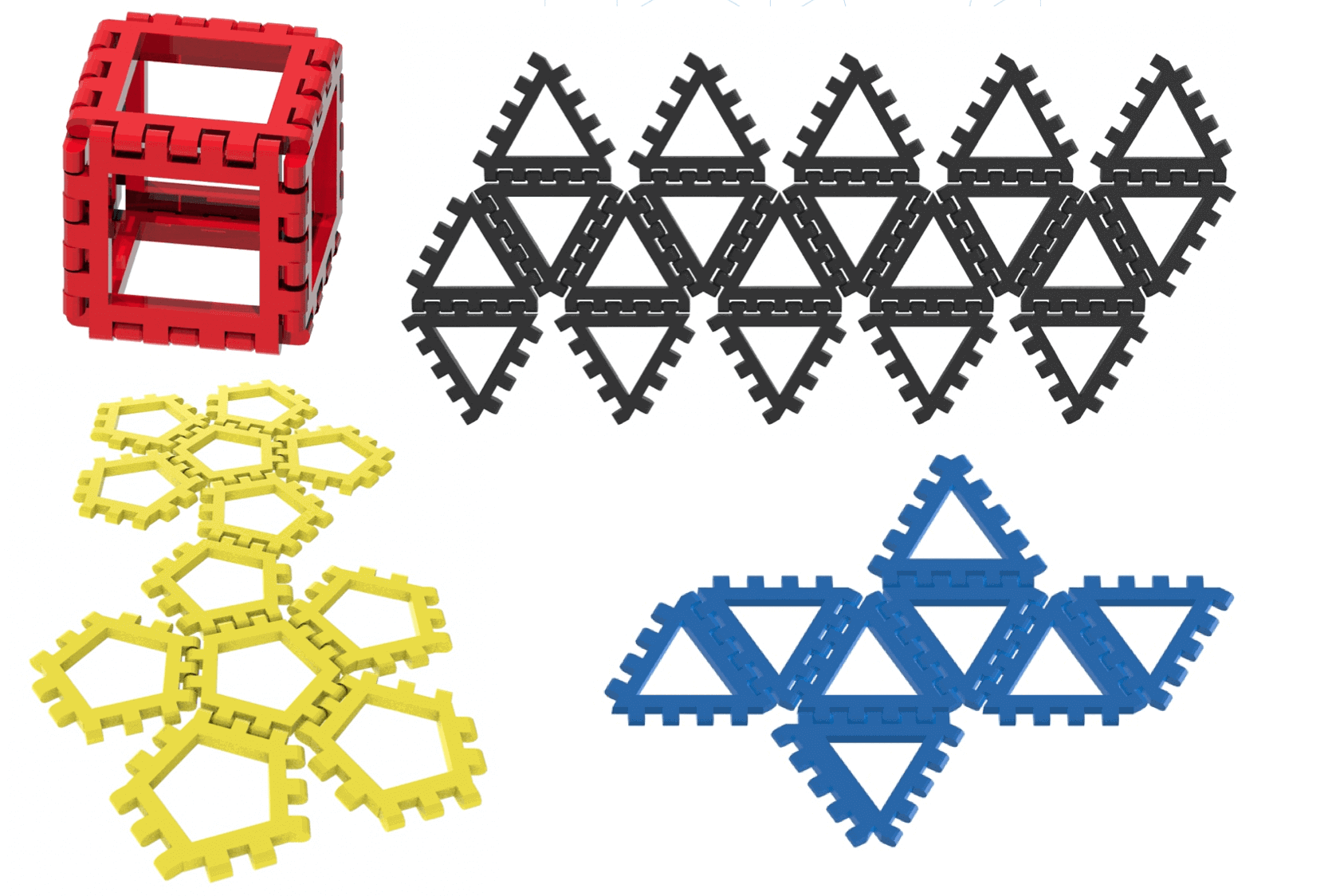
Each platonic solid can be constructed through the union of a certain number of equal geometric figures. The connection between the various elements will be made through comb joints.

Number of pieces of which the model is composed:

1) Tetrahedron – 4 equilateral triangles.
2) Hexahedral – 6 squares.
3) Octahedron – 8 equilateral triangles.
4) Dodecahedron – 12 pentagons.
5) Icosahedron – 20 equilateral triangles.

Suitable dimensions for its use in the classroom (mm):

1) Tetrahedron – 1 equilateral triangle 60x60x60 mm.
2) Hexahedral – 1 square 60x60x60 mm.
3) Octahedron – 1 triangle 60x60x60 mm.
4) Dodecahedron – 1 60 mm base pentagon.
5) Icosahedron – 1 triangle 60x60x60 mm.

Additional Material

Models used:

License Info

You are free to:

Share — copy and redistribute the material in any medium or format
Adapt — remix, transform, and build upon the material
for any purpose, even commercially.

Under the following terms:

Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.