Technichal Specifications
How to use this exercise?
The function of the model is to explain geometrically the Newton's binomial theorem for exponents 2 and 3.
Number of pieces of this exercise
9
General description
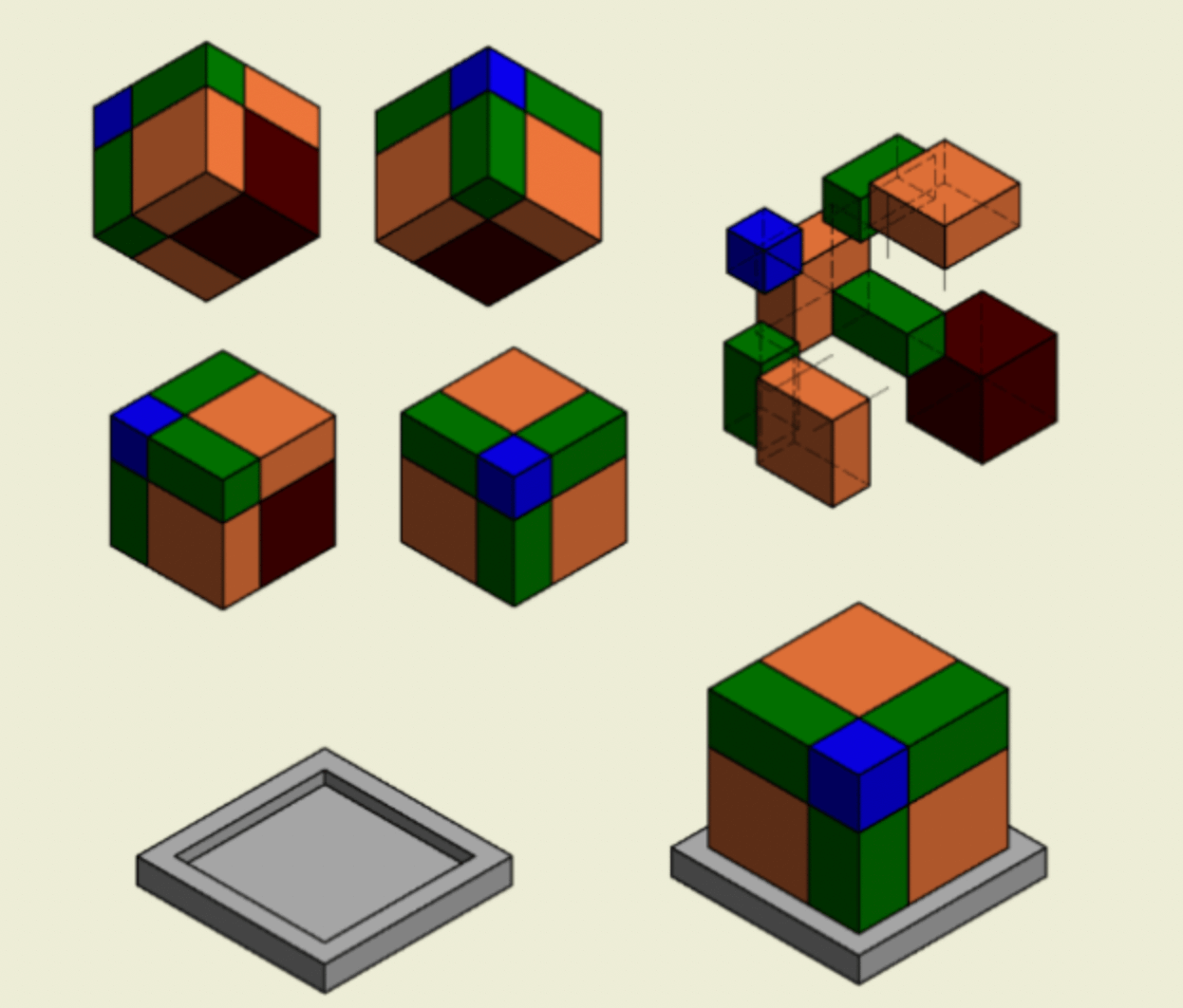
The model is composed of 8 parallelepipeds and a square base, which together in the appropriate way form a cube.
Pieces:
1 cube of dimensions a3.
1 cube of dimensions b3.
3 rectangular parallelepipeds of dimensions a2xb.
3 rectangular parallelepipeds of axb2 dimensions.
A square base to support it. (a+b+1.5cm)2
Additional Material
Models used:
License Info
Attribution 4.0 International (CC BY 4.0) https://creativecommons.org/licenses/by/4.0/You are free to:
Share — copy and redistribute the material in any medium or format
Adapt — remix, transform, and build upon the material
for any purpose, even commercially.
Under the following terms:
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.
Learning Specifications
How can the model be used in class?
The binomial theorem is a fundamental theorem of algebra that is used to expand expressions of the form: (a + b) n, where n can be any natural number.
Due to the abstract nature of the expression, this 3D model can help the student to have a geometrical understanding of this formula for exponents 2 and 3.
By strengthening this knowledge, the student will be able to delve in the theory and develop formulas for any value of n, while providing an intuitive understanding of the Pascal’s triangle.
What benefits can its use have?
– Help students who have difficulties to visualize equations.
– Improve the spatial vision of the student.
– Capture the attention of those students who are not interested in mathematics.
Can it be used in other subjects?
Any subject that needs the understanding of this formula, such as physics.