Tehnične specifikacije
Kako uporabljati to vajo?
Funkcija modela je geometrično razložiti Newtonov binomski izrek za eksponente 2 in 3.
Število kosov te vaje
9
Splošen opis
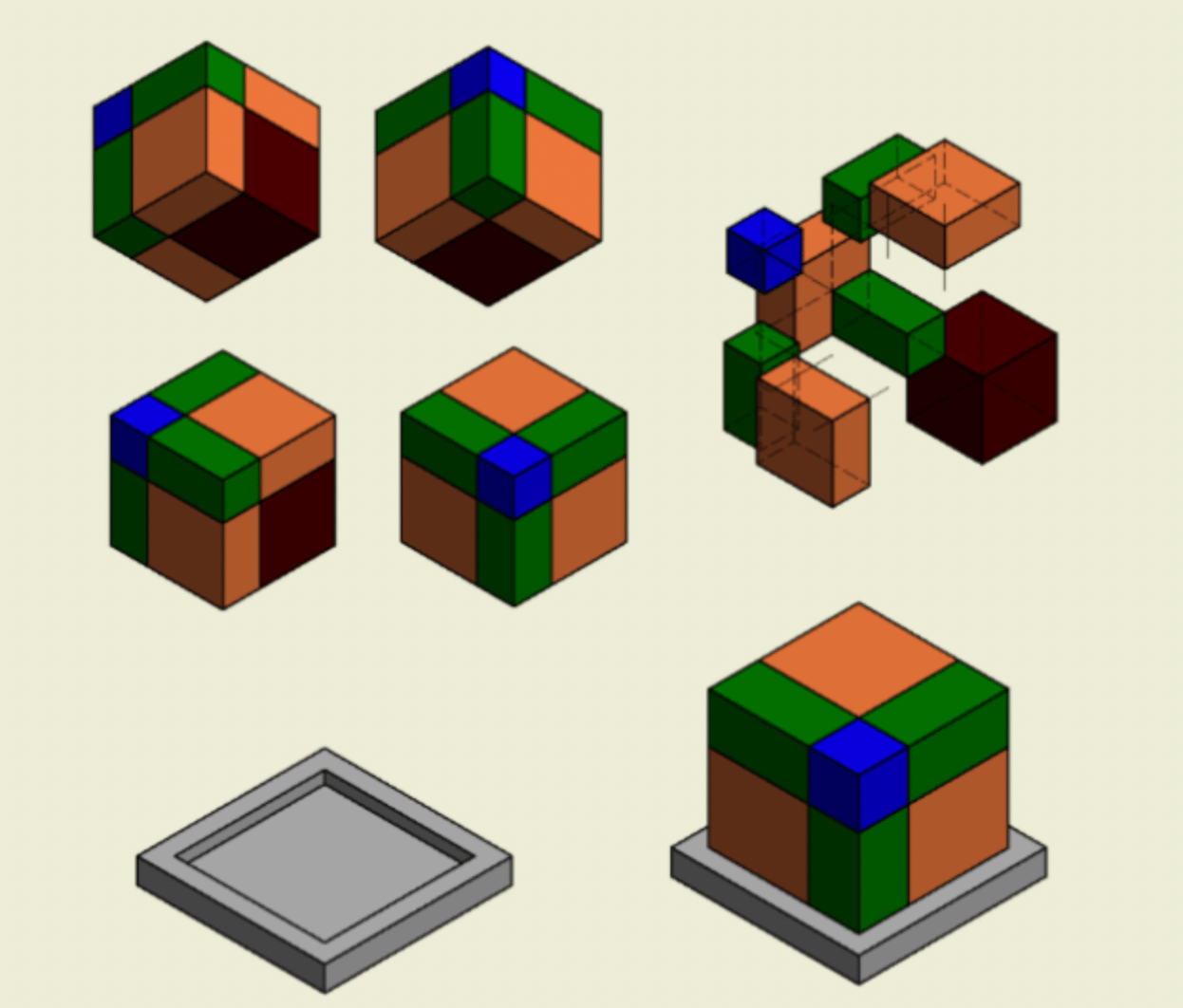
| Model je sestavljen iz 8 paralelepipedov in kvadratne osnove, ki na ustrezen način tvorijo kocko.
Kosi: 1 kocka dimenzij a^3. 1 kocka dimenzij b^3. 3 pravokotni paralelepipedi dimenzij a^2xb. 3 pravokotni paralelepipedi dimenzij axb^2. |
Kvadratna podlaga za podporo. (a + b + 1,5 cm)^2
Dodatni material
Uporabljeni modeli:
Informacije o licenci
4.0 Mednarodna dodeljevanja (CC 4,0) https://creativecommons.org/licenses/by/4.0/You are free to:
Share — copy and redistribute the material in any medium or format
Adapt — remix, transform, and build upon the material
for any purpose, even commercially.
Under the following terms:
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.
Specifikacije učenja
Kako se model lahko uporablja v razredu?
Binomski izrek je temeljni izrek algebre, ki se uporablja za razširitev izrazov oblike: (a + b) n, kjer je n lahko katerokoli naravno število.
Zaradi abstraktne narave izraza lahko ta 3D model pomaga študentu pridobiti geometrijsko razumevanje te formule za eksponente 2 in 3.
S krepitvijo tega znanja bo študent lahko poglobil teorijo in razvil formule za vsako vrednost n, obenem pa zagotovil intuitivno razumevanje Pascalovega trikotnika.
koristi za klobuke ima lahko njegova uporaba?
– Pomagati študentom, ki imajo težave z vizualizacijo enačb.
– Izboljšati prostorsko zavedanje učenca.
– Pridobiti pozornost tistih študentov, ki jih matematika ne zanima.
Ali se lahko uporablja tudi pri drugih predmetih?
Vsak predmet, ki potrebuje razumevanje te formule, kot je na primer fizika.